参考答案：8，2

解析： 依题意，β₁，β₂，β₃和α₁，α₂，α₃有相同的秩，α₁，α₂，α₃是3个具体的向量，容易求出α₁，α₂，α₃的秩，也就是β₁，β₂，β₃的秩，由此可以建立a，b的一个关系式．再由条件β₁可以由α₁，α₂，α₃线性表出，求出a，进一步求出b的值．
其中β₁可由以α₁，α₂，α₃线性表出，意味着方程组x₁α₁+x₂α₂+x₃α₃=β₁有解，因此，系数矩阵的秩等于增广矩阵的秩．做题时，可以把求a和求α₁，α₂，α₃的秩合成一步来做．
本题也可以这样做，容易看出α₁和α₂是线性无关的．如果α₁，α₂，α₃构成的行列式等于0，则α₁，α₂，α₃的秩为2，且α₁和α₂是一个极大线性无关组，如果行列式不等于0，则秩为3．因此判断向量组的秩可以通过行列式的计算．又因为β₁可以由α₁，α₂，α₃线性表出，那么β_I就可以由α₁，α₂，α₃的极大线性无关组线性表出，即可由α₁和α₂线性表出，于是β₁，α₁，α₂就线性相关，它们构成的行列式等于0．最后，β₁，β₂，β₃线性相关，β₁，β₂，β₃构成的行列式等于0．这种做法需要计算3个行列式．
方法1° 由题设知β₁可以由α₁，α₂，α₃线性表出，于是由

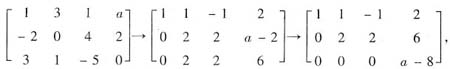
得到a-8=0，即a=8，且向量组α₁，α₂，α₃的秩为2．
依题意，β₁，β₂，β₃的秩也是2，β₁，β₂，β₃线性相关，它们构成的行列式等于0，即

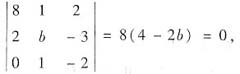
所以，b=2．
方法2° 因为

所以α₁，α₂，α₃线性相关，显然义有α₁，α₂线性无关，于是可知α₁，α₂，α₃的秩等于2，且α₁，α₂是一个极大线性无关组．
依题设β₁可以由α₁，α₂，α₃线性表出，β₁就可以由α₁，α₂线性表出，因而β₁，α₁，α₂线性相关，于是

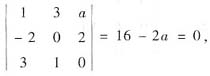
解得a=8．
依题意，β₁，β₂，β₃的秩也是2，β₁，β₂，β₃线性相关，它们构成的行列式等于0，即解得b=2．