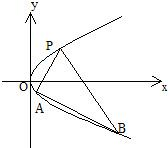
已知抛物线关于x轴对称,它的顶点是坐标原点,点P(2,4),A(x1,y1),B(x2,y2)是抛物线上的三点.
(Ⅰ)求该抛物线的方程;
(Ⅱ)若直线PA与PB的倾斜角互补,求线段AB中点的轨迹方程;
(Ⅲ)若AB⊥PA,求点B的纵坐标的取值范围.
(I)由已知条件,可设抛物线的方程为y2=2px,
∵点P(2,4)在抛物线上∴42=2p×2,得p=4,
故所求抛物线的方程是y2=8x.
(II)设直线PA的斜率为kPA,直线PB的斜率为kPB
则 kPA=(x1≠1),kPB=(x2≠1),
∵PA与PB的斜率存在且倾斜角互补,∴kPA=-kPB.
由A(x1,y1),B(x2,y2)在抛物线上,得y12=8x1 (1),y22=8x2 (2),
∴=-,∴y1+4=-(y2+4),∴y1+y2 =-8.
设AB的中点坐标为(x,y),则 y==-4,x===
=. 由题意知,y1<0,y2<0,
(-y1)+(-y2)=8>2,∴y1y2<16,∴>=2,即 x>2,
故线段AB中点的轨迹方程为 y=-4( x>2 ).
(III)由题意得 A(,y1)、B(,y2),故kAP ==,
由于AB⊥AP,∴kAB =-().又 KAB==,
∴y12+(y2+4)y1+4y2+64=0.
由△≥0,解得y2≤-12或y2≥20,故点B的纵坐标的取值范围是 (-∞,12]∪[20,+∞).