已知定义在R上的函数y=f(x)满足条件:对于任意的x,y∈R,f(x+y)=f(x)+f(y),当x>0时,f(x)<0。(1)求f(0)的值;
(2)讨论f(x)的奇偶性和单调性;
(3)当x>0时,对于f(x)总有f(1-m)+f(1-m2)<0,求m的取值范围。
解:(1)取x=y=0,得 ,
,
∴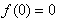 。
。
(2)取y=-x,则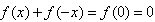 ,
,
∴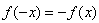 ,即
,即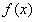 为奇函数;
为奇函数;
设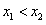 ,则
,则
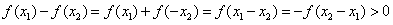 ,
,
所以,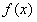 在R上单调递减。
在R上单调递减。
(3)f(1-m)+f(1-m2)<0,
∵f(0)=0,
∴f(1-m)+f(1-m2)<f(0),
∵f(x+y)=f(x)+f(y),
∴f(1-m+1-m2)<f(0),
∵f(x)在R上单调递减,当x>0时,对于f(x)总有f(1-m)+f(1-m2)<0,
∴原不等式的解集等价于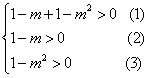 ,
,
化简,得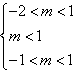 ,即-1<m<1,
,即-1<m<1,
∴m的取值范围是(-1,1)。

