问题
单项选择题
已知向量组α1,α2,α3线性无关,则下列向量组中线性无关的是
(A) α1,3α3,α1-2α2. (B) α1+α2,α2-α3,α3-α1-2α2.
(C) α1,α3+α1,α3-α1. (D) α2-α3,α2+α3,α2.
答案
参考答案:A
解析: 方法一 对于(A):设有数k1,k2,k3,使得
k1α1+k2(3α3)+k3(α1-2α3)=0,
即 (k1+k3)α1-2k3α2+3k2α3=0.
因为α1,α2,α3线性无关,敝k1+k3=0,2k3=0,3k2=0.可得k1=0,k2=0,k3=0.所以α1,3α3,α1-2α2线性无关.故选(A).
类似方法可判断(B),(C),(D)中向量组均线性相关.
方法二 因为
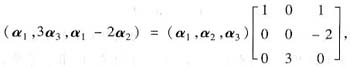
而
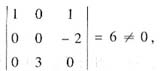
由α1,α2,α3线性无关可知α1,3α3,α1-2α2线性无关.故应选(A).
