问题
填空题
设R3中的两组基为ξ1=(1，0，0)T，ξ2=(-1，1，0)T，ξ3=(1，-2，1)T；η1=(2，0，0)T，η2=(-2，1，0)T，η3=(4，-4，1)T，则由基ξ1，ξ2，ξ3到η1，η2，η3的过渡矩阵为______．已知向量α=(2，3，-1)T，则α在基ξ1，ξ2，ξ3和基η1，η2，η3下的坐标分别为______．在两组基下有相同坐标的非零向量为______．
答案
参考答案：
，
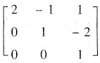，k(1，1，0)T，其中k为任意非零常数
解析： (Ⅰ)设(η1，η2，η3)=(ξ1，ξ2，ξ3)A，则过渡矩阵
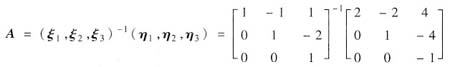
(Ⅱ)设α在基ξ1，ξ2，ξ3下的坐标x=(x1，x2，x3)T，则
α=x1ξ1+x2ξ2+x3ξ3，
即
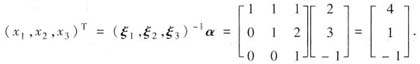
设α在基η1，η2，η3下的坐标为y1，y2，y3，则
α=y1η1+y2η2+y3η3．
同理可求出α=(2，-1，-1)T．
如果利用前面已求出的过渡矩阼，也可求出α在基ξ1，ξ2，ξ3下的坐标
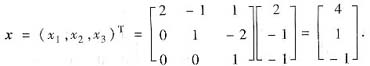
(Ⅲ)设所求向量为x=(x1，x2，x3T)，则
x=(ξ1，ξ2，ξ3)(x1，x2，x3)T=(η1，η2，η3)(x1，x2，x3)T
=(ξ1，ξ2，ξ3)A(x1，x2，x3)T．
所以 (ξ1，ξ2，ξ3)(x1，x2，x3)T=(ξ1，ξ2，ξ3)A(x1，x2，x3)T．
那么(x1，x2，x3)T=A(x1，x2，x3)T，即(A-E)(x1，x2，x3)T=0，于是有
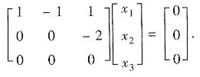
所以x=(x1，x2，x3)T=k(1，1，0)T，其中k为任意非零常数．