参考答案：B

解析： 命题①错误，因为只有对任意一组不全为零的数x₁，x₂，…，x_s，使向量组α₁，α₂，…，α_s的线性组合x₁α₁+x₂α₂+…+x_sα_s≠0时，才能说明向量组α₁，α₂，…，α_s线性无关．例如：向量组

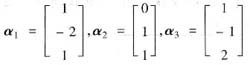
线性相关，但有2α₁+0α₂+0α₃≠0．
命题②错误．因为只有当数x₁，x₂，…，x_s全为零时，才能有线性组合x₁α₁+x₂α₂+…+x_sα_s=0，才说明向量组α₁，α₂，…，α_s线性无关，而对全为零的数x₁，x₂，…，x_s，任意s个向量构成的向量组α₁，α₂，…，α_s都有x₁α₁+x₂α₂+…+x_sα_s=0．例如：

易知α₁，α₂线性相关，β₁，β₂线性无关，但0α₁+0α₂=0，0β₁+0β₂=0．
命题③正确．因为线性无关的向量组的任意部分向量组都线性无关，所以必要性成立．反之，取t=s，则α₁，α₂，…，α_s线性无关，充分性也成立．
命题④错误．由③可知，向量组α₁，α₂，…，α_s中任意部分向量组都线性无关时，才可得向量组α₁，α₂，…，α_s线性无关．例如：向量组

其中α₁，α₂；α₂，α₃；α₃，α₁都线性无关(常称任意两个向量都线性无关的向量组是两两无关的)，但α₁，α₂，α₃线性相关，此即所谓两两无关的向量组不一定线性无关，但线性无关的向量组一定是两两无关的．
命题⑤错误．因为向量组α₁，α₂，…，α_s中任一向量都不能由其余向量线性表示时，才可得出α₁，α₂，…，α_s线性无关的结论．例如：向量组

线性相关，但α₃不能由α₁，α₂线性表示，α₂可由α₁，α₃线性表示．
命题⑥正确．因为如果α₁，α₂，…，α_s-1线性无关，由于α₁，α₂，…，α_s线性相关，所以α_s一定可以由α₁，α₂，…，α_s-1线性表示．
综上分析，应选(B)．