问题
问答题
确定常数a,使向量组(Ⅰ):
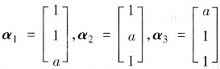 与向量组(Ⅱ):
与向量组(Ⅱ):
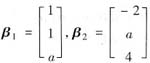 ,β3
,β3
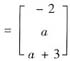 等价.
等价.
答案
参考答案:向量组(Ⅰ)与(Ⅱ)等价的含义是,向量组α1,α2,α3与向量组β1,β2,β3可以互相线性表出,也即以矩阵A=(α1,α2,α3)为系数阵且右端向量分别为β1,β2,β3的线性方程组有解,同时以矩阵B=(β1,β2,β3)为系数阵且右端向量分刖为α1,α2,α3的线性方程组有解.可求得
(1)当a≠-2且a≠1时,|A|≠0,|B|≠0,即r(A)=r(B)=3,从而向量组(Ⅰ)与(Ⅱ)的秩都是3,即线性无关.而任意4个3维向量都是线性相关的,故它们可以互相线性表出,即向量组(Ⅰ)与(Ⅱ)等价.
(2)当a=1时,可求得r(A)=1,r(B)=2,即向量组(Ⅰ)的秩为1,而向量组(Ⅱ)的秩为2,故向量组(Ⅰ)与(Ⅱ)不等价(等价的向量组有相同的秩).
(3)当a=-2时,有

可见β3不能由α1,α2,α3线性表出,故向量组(Ⅰ)与(Ⅱ)不等价.
综上所述知,当a≠1且a≠-2时,向量组(Ⅰ)与(Ⅱ)等价.
