(1)设n维向量组(Ⅰ)α1，α2，…，αs，(Ⅱ)β1，β2，…，βt，证明：向量组(Ⅰ)和(Ⅱ)是等价向量组的充分必要条件是r(α1，α2，…，αs)=r(α1，α2，…，αs，β1，β2，…，βt)=r(β1，β2，…，βt)；
(2)设向量组α1=(1，-2，1)T，α2=(2，1，5)T，α3=(3，-1，6)T；向量组β1=(-2，1+a，4)T，β2=(1，3，4)T，问a为何值时向量组α1，α2，α3与向量组β1，β2，β3是等价向量组；a为何值时，不是
参考答案：(1)向量组α1，α2，…，αs与向量组β1，β2，…，βt等价
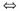αi(i=1，2，…，s)可由β1，β2，…，βt线性表出，且βj(j=1，2，…，t)可由α1，α2，…，αs线性表出
α1，α2，…，αs的极大线性无关组也是向量组α1，α2，…，αs，β1，β2，…，βt的极大线性无关组，且向量组β1，β2，…，βt的极大线性无关组也是向量组β1，β2，…，βt，α1，α2，…，αs的极大线性无关组
r(α1，α2，…，αs)=r(α1，α2，…，αs，β1，β2，…，βt)，且r(β1，β2，…，βt)=r(β1，β2，…，βt，α1，α2，…，αs)
r(α1，α2，…，αs)=r(α1，α2，…，αs，β1，β2，…，βt)=r(β1，β2，…，βt)．
(2)将(α1，α2，α3；β1，β2)一起作初等行变换，即
1)当a=13时，因
r(α1，α2，α3)=r(α1，α2，α3
β1，β2)=r(β1，β2)=2，
故α1，α2，α3与β1，β2是等价向量组．
2)当a≠13时，因r(α1，α2，α3)=r(β1，β2)=2≠r(α1，α2，α3，β1，β2)=3，故α1，α2，α3与β1，β2不是等价向量组．