设有两个向量组α1,α2,…,αs和β1,β2,…,βt,且r(α1,α2,…,αs)=r(β1,β2,…,βt),则下列结论正确的是
(A) 两个向量组等价.
(B) 当α1,α2,…,αs能由β1,β2,…,βt线性表出时,两个向量组等价.
(C) 当s=t时,两个向量组等价.
(D) 当r(α1,α2,…,αs,β1,β2,…,βt)=r(α1,α2,…,αs)+r(β1,β2,…,βt)时,两向量组等价.
参考答案:B
解析: 等价向量组与其秩的关系的结论:向量组α1,α2,…,αs与β1,β2,…,βt等价jr(α1,α2,,…,αs)=r(β1,β2,…,βt).
设r(α1,α2,…,αs)=r(β1,β2,…,βt)=r,且
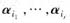 与
与
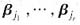 分别是向量组α1,α2,…,αs和β1,β2,…,βt的极大无关组,由α1,α2,…,αs能由β1,β2,…,βt线性表出知
分别是向量组α1,α2,…,αs和β1,β2,…,βt的极大无关组,由α1,α2,…,αs能由β1,β2,…,βt线性表出知
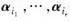 可由
可由
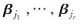 线性表出,即有
线性表出,即有
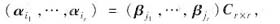
其中C为表出系数矩阵,且r(C)=r.
事实上,由于
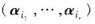 是
是
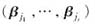 与C的乘积,因此有
与C的乘积,因此有
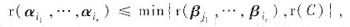
即 r≤min{r,r(C)}.
由此有r(C)≥r,且C为r×r矩阵,只有r(C)≤r,故r(C)=r,C为可逆矩阵.所以有
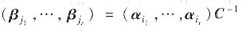
由此可知
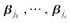 可由
可由
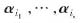 线性表出.
线性表出.
由于
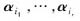 和
和
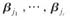 可互相线性表出,故两个向量组等价,又由于向量组与其极大无
可互相线性表出,故两个向量组等价,又由于向量组与其极大无
关组等价,据等价的传递性可推出向量组α1,α2,…,αs和β1,β2,…,βs为等价向量组.故应选(B).
