参考答案：A

解析： 判断向量组线性无关最基本的思路就是：方法1°定义法．方法2°列向量线性无关，也就是矩阵的列满秩，证明B的秩为n．方法3°B列满秩，那么齐次线性方程组Bx=0只有零解．
方法1°设B=(b₁，b₂，…，b_n)，考虑
x₁b₁+x₂b₂+…+x_nb_n=0，
等式两边同时左乘矩阵A，有
x₁Ab₁+x₂Ab₂+…+x_nAb_n=0，
由AB=E，有

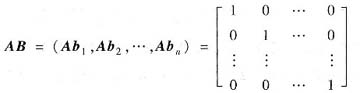
即

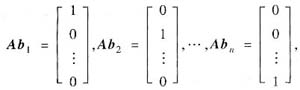
代入，得

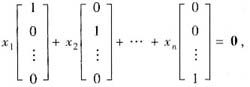
即 (x₁，x₂，…，x_n)=0，
所以，b₁，b₂，…，b_n线性无关，即B的列向量线性无关．故③正确．同理可证①正确．故应选(A)．
方法2°依题意有 r(AB)=r(E)=n．
由矩阵的秩的性质，有 n=r(AB)≤r(B)，
又B是m×n矩阵，即有 r(B)≤n，所以 r(B)=n．
从而可知B的列向量线性无关．故③正确．同理可证①正确．应选(A)．
方法3° 考虑齐次线性方程组Bx=0，等式两边同时左乘矩阵A，得
ABx=0．
代入AB=E，得 x=0．
齐次线性方程组只有零解，故系数矩阵列满秩，B的列向量线性无关．由此可知③正确．同理可证①正确．应选(A)．