问题
问答题
一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4.
(1)从袋中随机取出两个球,求取出的球的编号之和不大于4的概率;
(2)先从袋中随机取一个球,该球的编号为m,将球放回袋中,然后再从袋中随机取一个球,该球的编号为咒,求n<m+2的概率.
答案
参考答案:
(1)从袋子中随机取两个球,其一切可能的结果组成的基本事件有1和2,1和3,1和4,2和3,2和4,3和4,共6个.
从袋中随机取出的球的编号之和不大于4的事件共有1和2,1和3两个.
因此所求事件的概率为
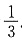
(2)先从袋中随机取一个球,记下编号为m,放回后,在从袋中随机取一个球,记下编号为n,其一切可能的结果(m,n)有:
(1,1)(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1)(3,2),(3,3)(3,4),(4,1)(4,2),(4,3)(4,4),共16个有满足条件n≥m+2的事件为(1,3)(1,4)(2,4),共3个.
所以满足条件n≥m+2的事件的概率为
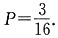
故满足条件n<m+2的事件的概率为
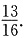

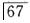 缺失,未萌,以下设计合理的是()
缺失,未萌,以下设计合理的是()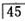 单端桥修复
单端桥修复 单端桥修复
单端桥修复 单端桥修复
单端桥修复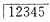 单端桥修复
单端桥修复