问题
问答题
如图：四棱锥P—ABCD中，底面ABCD是矩形，PA上底面ABCD，PA=AB=1，
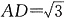，点F是PB的中点，点E在边BC上移动．
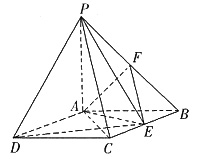
(1)点E为BC的中点时，试判断EF与平面PAC的位置关系，并说明理由；
(2)证明：无论点E在BC边的何处，都有PE⊥AF；
(3)当BE等于何值时，PA与平面PDE所成角的大小为45°．
答案
参考答案：
解法一：(1)当点E为BC的中点时，EF与平面PAC平行，
∵在△PBC中，E、F分别为BC、PB的中点，
∴EF∥PC又
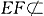平面PAC，
而
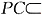平面PAC∴EF∥平面PAC.
(2)证明：∵PA⊥平面ABCD，
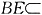平面ABCD，
∴EB⊥PA. 又EB⊥AB，AB∩AP=A，AB，
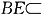平面PAB，
∴EB⊥平面PAB，
又
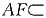平面PAB，∴AF⊥BE.
又PA=AB=1，点F是PB的中点，∴AF⊥PB，
又∵PB∩BE=B，PB，
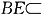平面PBE，∴AF⊥平面PBE.
∵
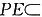平面PBE，∴AF⊥PE.
(3)过A作AG⊥DE于G，连PG，又∵DE⊥PA，则DE⊥平面PAG，
于是，平面PAG⊥平面PDE，它们的交线是PG，过A作AM⊥PG，垂足为M，则AM⊥平面PDE，即PA在平面PDE的射影是PM，所以PA与平面PDE所成的角是∠APG=45°，
∴在Rt△PAG中，PA=AG=1，∴
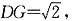
设BE=x，∵△AGE≌△ABE，则GE=x，
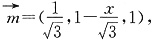
在Rt△DCE中，
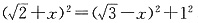，得
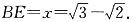
解法二：(2)建立图示空间直角坐标系，
则P(0，0，1)，B(0，1，0)，
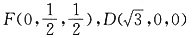设BE=x，则E(x，1，0)
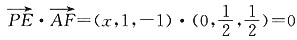，∴AF⊥PE
(3)设平面PDE的法向量为
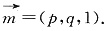由
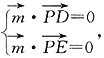得：
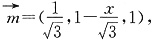
而
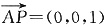依题意PA与平面PDE所成角为45°，
所以
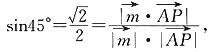
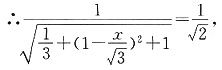
得
，或
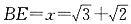(舍)．