问题
问答题
已知A，B是△ABC的两个内角，
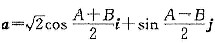(其中i，j是互相垂直的单位向量)，若
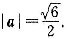
求tanC的最大值，并判断此时三角形的形状．
答案
参考答案：
∵tanAtanB= 1/3 ＞0，∴tanA＞0，tanB＞0
∴tan（A+B）= tanA+tanB/1-tanAtanB = 3 /2 （tanA+tanB）≥ 3/2 ×2
= 
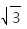
∴tan（A+B）≥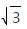 
，即-tanC≥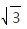
∴tanC≤-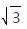 
当tanC=-
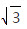时， tanA+tanB= 2
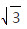/3 tanA•tanB= 1/3 ，即tanA=tanB= 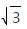3
∴A=B=30°
∴tanC的最大值为-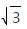 ，此时△ABC为等腰三角形