【说明】
计算三角函数sinx
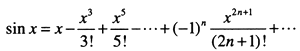
给定精度e和n,若第k步后的结果为sin1,第k+1步后的结果为sin2,若|sin1·sin2|<e,则返回sin1的值。若没有达到精度e,但是步骤达到n步,则返回第n步后的值。其流程图如下所示:
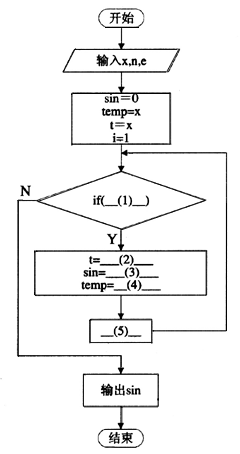
参考答案:(1)i<=n && abs(sin-temp)>e (2)-t*x*x/((2*i)*(2*i+1)) (3)temp
(4)sin+t (5)i++
解析:
[分析]:
本题考查程序流程图对三角函数sinx的计算。
首先我们来分析一下三角函数sinx的计算过程。对三角函数sinx的计算是根据题目中给出的展开式来进行的,每次计算是在原来的基础上加上一项,其初始项为x。通过判断第k步与第k+1步结果的差的绝对值与精度e的大小来决定计算是否继续。如果结果的差大于精度e,计算继续,反之则停止。再有就是如果结果的差一直大于精度e,则计算到n步后停止。由上述描述我们知道,对三角函数sinx的计算需要一个条件循环,且循环的条件应该是第k步与第k+1步结果的差与精度e的大小关系和计算步数与n的大小关系。
下面,我们来看程序流程图。在流程图中,首先是输入x,e,n的值,接下来申请了几个临时变量sin,temp,i,t。第(1)空在条件循环的开始处,很明显是要填控制循环的条件,由上面的分析我们知道,循环的条件应该是第k步与第k+1步结果的差的绝对值与精度 e的大小关系和计算步数与n的大小关系,但是,在此处我们还没弄清楚变量sin,temp,i,t分别用于存放什么内容,因此,此空最好是在做完后面的以后再回头来完成。
第(2)空处是要将一个值赋给变量t,变量t的初始赋值语句是t=x,这是将展开式的第一项赋给了变量t,因此变量t有可能是用来存放第1步的运算结果,也很有可能用来存放每次要加的项。结合这个流程图来看,变量t中存放的是每次要加的项,确定了这个后,再结合展开式中第k项与第k+1项的特点和通项公式,不难看出第(2)空应该填-t*x*x/((2*i)*(2*i+1))。
第(3)空是紧接着第(2)空而来,是将一个值赋给变量sin,变量sin的初始赋值语句是sin=0,结合整个流程可以知道,第(3)空与第(4)空应该结合起来完成,变量 sin与temp分别用于存放第k步与第k+1步的运算结果,由它们的初值我们可以判断出,变量sin用来存放第k步的运算结果,而temp用来存放第A步的运算结果与增加项的和,即第k+l步的运算结果。在每次运算前,我们都把其结果保存在变量sin中。因此,第 (3)空的答案为temp,第(4)空的答案为sin+t。
结合程序全过程来看,可以知道第(5)空处是用来控制计算步数的。每计算一次后程序的计算步数应该就增加了1,在流程图中,变量i是用来统计计算步数的,因此,第(5)空的答案是i++。
在知道变了量sin,temp,i,t的作用后,第(1)空就很简单了,答案应该为i<=n && abs(sin-temp)>e。
