问题
填空题
| 若对任意x∈A,y∈B,(A⊆R,B⊆R)有唯一确定的f(x,y)与之对应,则称f(x,y)为关于x,y的二元函数. 定义:满足下列性质的二元函数f(x,y)为关于实数x,y的广义“距离”: (1)非负性:f(x,y)≥0,当且仅当x=y时取等号; (2)对称性:f(x,y)=f(y,x); (3)三角形不等式:f(x,y)≤f(x,z)+f(z,y)对任意的实数z均成立. 给出三个二元函数:①f(x,y)=(x-y)2;②f(x,y)=|x-y|; ③f(x,y)=
请选出所有能够成为关于x,y的广义“距离”的序号______. |
答案
对于①,不妨令x-y=2,则有x-
=x+y 2
-y=1,此时有(x-y)2=4,而 (x-x+y 2
)2=( x+y 2
-y)2=1,故f(x,y)≤f(x,z)+f(z,y)不成立,所以不满足三角不等式,故①不满足x+y 2
对于②,f(x,y)=|x-y|≥0满足(1);f(x,y)=|x-y|=f(y,x)=|y-x|满足(2);f(x,y)=|x-y|=|(x-z)+(z-y)|≤|x-z|+|z-y|=f(x,z)+f(z,y)满足(3),故②能够成为关于的x、y的广义“距离”的函数
对于③,由于x-y>0时,f(y,x)=
无意义,故③不满足y-x
故答案为:②

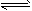 C(g)+D(g)过程中的能量变化如图所示,回答下列问题
C(g)+D(g)过程中的能量变化如图所示,回答下列问题