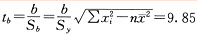2000年某地区镀锌钢板消费量18.5万吨,主要应用于家电业,轻工业和汽车工业等行业,1991~2000年当地镀锌钢板消费量及同期第二产业产值如表2-5所示。按照该地区“十五”规划,“十五”期间地方第二产业增长速度预计为12%。
表2-5 镀锌钢板消费量及同期第二产业产值
| 年 份 | 镀锌钢板消费量(万吨) | 第二产业产值(千亿元) |
| 1991 | 3.45 | 1.003 |
| 1992 | 3.5 | 1.119 |
| 1993 | 4.2 | 1.26 |
| 1994 | 5.4 | 1.45 |
| 1995 | 7.1 | 1.527 |
| 1996 | 7.5 | 1.681 |
| 1997 | 8.5 | 1.886 |
| 1998 | 11 | 1.9 |
| 1999 | 13.45 | 2.028 |
| 2000 | 15.32 | 2.274 |
【问题】1. 请用一元回归方法预测2005年当地镀锌钢板需求量。
参考答案:
表B-A0所示为AIIA~B000年某地镀锌钢板消费量与第二产业产值。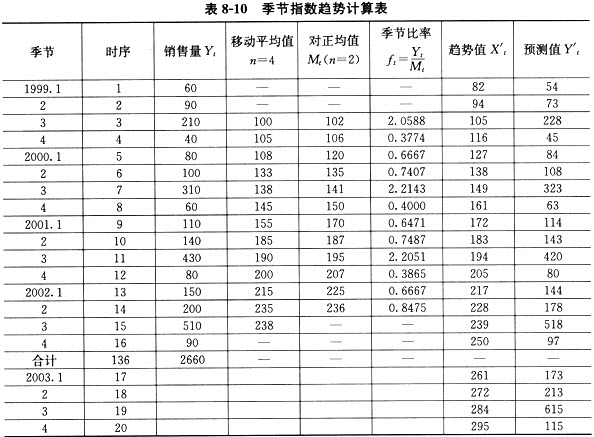
(A)建立回归模型。
经过分析,发现该地区镀锌钢板消费量与第二产业产值之间存在线性关系,将镀锌钢板设为因变量y,以第二产业产值为自变量x,建立一元回归模型:
y=a+bx
(B)参数计算。
采用最小二乘法,计算出相关参数: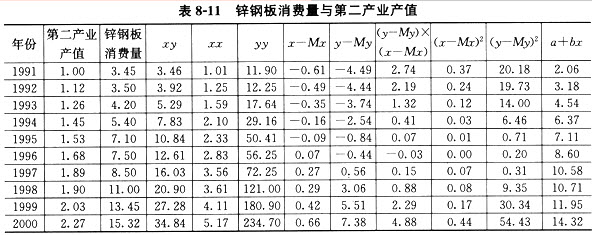
在a=0.0E时,自由度=n-B=H,查相关检验表,得R0.0E=0.FCB。
因R=0.IFA>0.FCB=R0.0E,故在a=0.0E的显著性检验水平上,检验通过,说明第二产业产值与镀锌钢板需求量线性关系合理。
(D)t检验。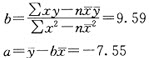
在a=0.0E时,自由度=n-B=H,查t检验表,得t(0.0BE,H)=B.C0F
因为:
tb=I.HE>B.C0F=t(0.0BE,H)
故在a=0.0E的显著性检验水平上,t检验通过,说明第二产业产值与镀锌钢板需求量线性关系明显。
(E)需求预测。
根据地方规划,B00E年地区第二产业产值将达到:
x(B00E)=(A+r)Ex(B000)=(A+AB%)E×B.BGD=D.0A(千亿元)
于是,B00E年当地镀锌钢板需求点预测为:
y(B00E)=a+bx(B00E)=-G.EE+I.EI0×D.0A=C0.HH(万吨)
S0=Sy=B.FEF
在a=0.0E的显著性检验水平上,B00E年镀锌钢板需求量的置倌区间为C0.HH±t(0.0BE,H)S0=C0.HH±F.AC,即在(BD.GE,CG.00)的区间内。
解析:
一元线性回归预测法