定义在R上的奇函数f(x),当x≥0时,f(x)=
|
当x<0时,函数的解析式是f(x)=
,log2(1-x),x∈(-1,0) |x+3|-x,x∈(-∞,-1)
故函数f(x)在x∈R上的图象如图所示,方程f(x)=
共有五个实根,最左边两根之和为-6,最右边两根之和为6,中间的一个根满足log2(1-x)=1 2
,即x=1-1 2
,故所有根的和为1-2
.2
故答案为:1-
.2
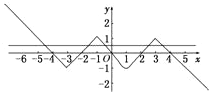
定义在R上的奇函数f(x),当x≥0时,f(x)=
|
当x<0时,函数的解析式是f(x)=
,log2(1-x),x∈(-1,0) |x+3|-x,x∈(-∞,-1)
故函数f(x)在x∈R上的图象如图所示,方程f(x)=
共有五个实根,最左边两根之和为-6,最右边两根之和为6,中间的一个根满足log2(1-x)=1 2
,即x=1-1 2
,故所有根的和为1-2
.2
故答案为:1-
.2
