问题
单项选择题
函数y1=f（a+x）（a≠0）与y2=f（a-x）的图像关于（）。
A．直线x-a=0对称
B．直线x+a=0对称
C．x轴对称
D．y轴对称
答案
参考答案：A
解析：
根据公式：f(x+a)与f(-x+b)图像关于直线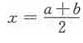
对称，所以函数y1=f(a+x)与y2=f(a-x)的图像关于直线x=a对称，故选A。
搜题请搜索小程序“爱下问搜题”
函数y1=f（a+x）（a≠0）与y2=f（a-x）的图像关于（）。
A．直线x-a=0对称
B．直线x+a=0对称
C．x轴对称
D．y轴对称
参考答案：A
解析：
根据公式：f(x+a)与f(-x+b)图像关于直线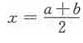对称，所以函数y1=f(a+x)与y2=f(a-x)的图像关于直线x=a对称，故选A。