问题
填空题
(本小题满分12分)
已知抛物线y2=mx的焦点到准线距离为1,且抛物线开口向右.
(Ⅰ)求m的值;
(Ⅱ)P是抛物线y2=mx上的动点,点B,C在y轴上,圆(x-1)2+y2=1内切于
△PBC,求△PBC面积的最小值.
答案
(1)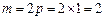
(2) 的最小值为8.
的最小值为8.
解:(Ⅰ)由题意知,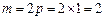 .……………………4分
.……………………4分
(Ⅱ)设 ,不妨设
,不妨设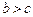 .直线
.直线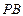 的方程:
的方程: ,
,
化简得 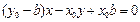 .
.
又圆心 到
到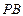 的距离为1,
的距离为1,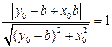 ,
,
故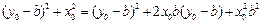 ,…………………6分
,…………………6分
易知 ,上式化简得
,上式化简得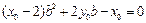 ,
,
同理有 .
.
所以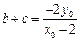 ,
, ,则
,则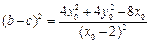 .……………8分
.……………8分
因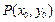 是抛物线上的点,有
是抛物线上的点,有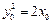 ,则
,则 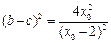 ,
,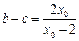 .
.
所以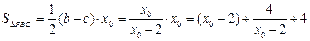
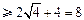 .……10分
.……10分
当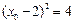 时,上式取等号.
时,上式取等号.
此时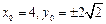 .∴
.∴ 的最小值为8.………………………… 12分
的最小值为8.………………………… 12分
