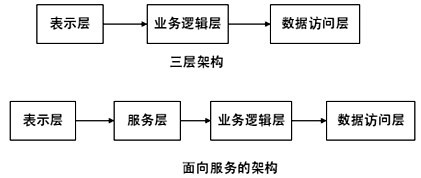
问题
问答题
设函数y(x)在任意点处的增量
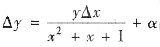 ,其中α是当△x→0时比△x较高阶的无穷小,且y(0)=π,则y(1)=______.
,其中α是当△x→0时比△x较高阶的无穷小,且y(0)=π,则y(1)=______.
答案
参考答案:首先尝试从△y的表达式直接求y(1).为此,设x0=0,△x=1,于是△y=y(x0+△x)-y(x0)=y(1)-y(0)=y(1)-π,代入△y的表达式即得
[*]
由于仅仅知道当△x→0时α是比△x较高阶的无穷小,而不知道α的具体形式,因而从上式无法求出y(1)来.
由此可见,为了求出y(1)必须去掉△y的表达式中包含的α.利用函数的增量△y与其微分dy的关系可知,函数y(x)在任意点x处的微分
[*]
这是一个可分离变量的方程,它的满足初始条件y|x=0=π的特解正是本题中所说的函数y(x),解出y(x)即可得到y(1).
将方程[*]分离变量,得[*]
求积分可得[*]
解出y得方程的通解[*]
扫初始条件 y(0)=π可确定[*],于是
[*]