问题
问答题
设f(x)在x=a的某邻域内具有n阶导数，且
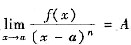，则f(a)=f’(a)=f"(a)=…=f(n-1)(a)=0，f(n)(a)=n!A．
答案
参考答案：[证明] 把f(x)的带皮亚诺余项的泰勒公式
[*]
代入可得
[*]
即
[*]
从而f(a)=f’(a)=…f(n-1)(a)=0，且
[*]
解析：
[*]
搜题请搜索小程序“爱下问搜题”
设f(x)在x=a的某邻域内具有n阶导数，且
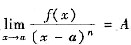，则f(a)=f’(a)=f"(a)=…=f(n-1)(a)=0，f(n)(a)=n!A．
参考答案：[证明] 把f(x)的带皮亚诺余项的泰勒公式
[*]
代入可得
[*]
即
[*]
从而f(a)=f’(a)=…f(n-1)(a)=0，且
[*]
解析：
[*]