问题
问答题
设一凸的光滑曲线连接O(0，0)，A(1，4)两点，而P(x，y)为曲线上任意一点，已知曲线与线段
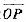所围平面图形的面积为
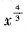，求该曲线的方程．
答案
参考答案：[分析与求解] 设曲线方程为y=y(x)．
1° 首先写出曲线y=y(x)与线段[*]所围平面图形面积S(x)的表达式．由于y=y(x)是凸的，所以O、P两点间的曲线在线段[*]上方，如图20-1所示，于是
[*]
按题意：[*]
2° 解含变限积分的方程——转化为微分方程．两边求导得
[*]②
(①式中令x=0时，等式自然成立，无须加其他附加条件，①与②等价)．化简得
[*]
解此一阶线性方程，两边乘[*]，积分得
[*]
3° 曲线经过点A(1，4)，即y(1)=4，由此可确定常数C=0．
故该曲线的方程为[*]．
[*]