问题
问答题
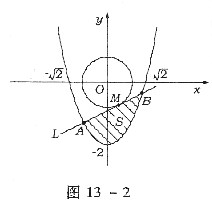
如图13-2，设单位圆x2+y2=1上点M(x0，y0)处的切线L与抛物线y=x2-2围成的图形的面积S达到最小，求点M的坐标和切线L的方程．
答案
参考答案：[解] 设切线L的方程为y=kx-b，其中b＞0(从几何图形知，当面积S最小时点M应位于单位圆的下半圆上，故可作以上假设)，则L与抛物线交点A和B的横坐标x1和x2应满足方程组
[*]
于是，L与抛物线所围成图形的面积
[*]
因为[*]
于是[*]
代入，即得[*]
从而，S与[*]在同一点上取得最小值．现考虑函数[*]
单位圆x2+y2=1在点M(x0，y0)处的切线L的方程是
[*]
即[*]，代入f的表达式得
[*]
于是[*]
对应的y0满足[*]，与y0相应的[*]即点M的坐标为[*]或[*]，[*]，过M的切线L的方程为[*]
