问题
问答题
求一阶差分方程2yt+1+yt=
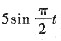满足y0=4的特解．
答案
参考答案：[解] 对应齐次差分方程的通解是[*]，其中C是任意常数；非齐次差分方程有形式为[*]=[*]的特解，代入方程得
[*]
可确定常数 A=1，B=-2．从而原方程的通解为
[*]
令t=0，利用初值y0=4又可确定C=6，故所求特解为
[*]
解析：
[*]
搜题请搜索小程序“爱下问搜题”
求一阶差分方程2yt+1+yt=
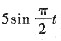满足y0=4的特解．
参考答案：[解] 对应齐次差分方程的通解是[*]，其中C是任意常数；非齐次差分方程有形式为[*]=[*]的特解，代入方程得
[*]
可确定常数 A=1，B=-2．从而原方程的通解为
[*]
令t=0，利用初值y0=4又可确定C=6，故所求特解为
[*]
解析：
[*]