问题
问答题
设a≠0为常数，f(x)在(-∞，+∞)连续，考察一阶线性常系数方程
y’+ay=f(x) (x∈(-∞，+∞))． (*)
(Ⅰ) 求通解的表达式；
(Ⅱ) 设a＞0，又f(x)有界且
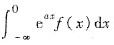收敛，求证：方程(*)只有一个解在(-∞，+∞)有界；
(Ⅲ) 若又有f(x)以T为周期，求证：方程(*)只有一个解是以T为周期的．
答案
参考答案：[分析与求解] (Ⅰ) 将方程两边乘以[*]得
(yeax)’=eaxf(x)．
积分得 yeax=∫eaxf(x)dx+C．
于是得通解
[*]
或[*]
其中C为[*]常数．通解即所有解．
(Ⅱ) 由通解表达式知
[*]
若[*]，则[*]，于是y(x)在(-∞，+∞)无界．
若[*]，即[*]，则相应的
[*]
即y(x)在(-∞，+∞)有界．
因此，(*)只有一个有界解(x∈(-∞，+∞))．
(Ⅲ) 若y(x)是(*)的以T为周期的解 [*]y(x)必是有界的[*]
[*]
以下只须再证：y(X)以T为周期．由
[*]
[*]y(X)以T为周期．
因此，(*)只有一个解是以T为周期的．