问题
问答题
设由曲线
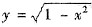与直线x=a(0＜a＜1)以及y=0，y=1围成的平面图形(如图的阴影部分)绕x轴旋转一周所得旋转体的体积为V(a)，求V(a)的最小值与最小值点．
答案
参考答案：[解法一] 由曲线[*]与直线x=a(0＜a＜1)以及y=0，y=1围成的平面图形可分为两个部分区域
[*]
在D1中x→x+dx的小窄条绕x轴旋转产生一个圆环形薄片，其内半径为[*]，外半径为y=1，厚度为dx，从而其体积[*]．故区域D1绕x轴旋转一周所得旋转体的体积
[*]
在D2中x→x+dx的小窄条绕x轴旋转产生一个圆形薄片，其半径为y=[*]，厚度为dx，从而其体积dV=π(1-x2)dx．故区域D2绕x轴旋转一周所得旋转体的体积
[*]
把V1(a)与V2(a)相加，即得
[*]
由于
[*]
故[*]，即V(a)的最小值是[*]，最小值点是[*]
[解法二] 由曲线[*]与直线x=a(0＜a＜1)以及y=0，y=1围成的平面图形可分为两个部分区域
[*]
在D1中y→y+dy的小窄条绕x轴旋转产生一个薄壁圆筒，其高度为[*]，半径为y，厚度为dy，从而其体积[*]．故区域D1绕x轴旋转一周所得旋转体的体积
[*]
在D2中y→y+dy的小窄条绕x轴旋转产生一个薄壁圆筒，其高度为[*]，半径为y，厚度为dy，从而其体积[*]，故区域D2绕x轴旋转一周所得旋转体的体积
[*]
把V1(a)与V2(a)相加，即得
[*]
以下同[解法一] ．
