问题
问答题
确定常数a和b>0的值,使函数
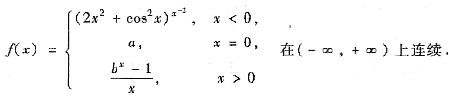
答案
参考答案:[解] 当x<0时,f(x)等于初等函数[*],由初等函数连续性知f(x)在(-∞,0)连续,且
[*]
当x>0时f(x)等于初等函数[*],由初等函数的连续性知f(x)在(0,+∞)连续,且
[*]
从而,为使f(x)在(-∞,+∞)上连续,必须且只需f(x)还在点x=0处连续,即
f(0-0)=a=f(0+0),[*]e=a=lnb.
故当a=e且b=ee时f(x)在(-∞,+∞)上连续.
解析:[*]
