问题
单项选择题
判断积分值的大小：
设
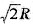，i=1，2，3，其中
D1={(x，y)|x2+y2≤R2}，D2={(x，y)|x2+y2≤2R2}，
D3={(x，y)||x|≤R，|y|≤R
答案
参考答案：C
解析：本题被积函数连续，恒正且相同，但积分区域不同，可通过比较积分区域的大小来判断积分值的大小．D1，D2均是以原点为圆心，半径分别为R，[*]的圆；D3是正方形，边长2R，如图17-1(b)所示， D1[*]D3[*]D2．因此(C)成立．
[*]