问题
问答题
设函数f(x)在(-∞,+∞)上连续,f(0)=0,且对任何x,t∈(-∞,+∞)满足
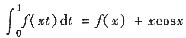 .
.
试求f(x)在(-∞,+∞)上的导函数f’(x).
答案
参考答案:[解] 当x≠0时,令xt≠=u,可得[*]
于是,当x≠0时[*]即[*]
由f(x)的连续性知[*]可导,从而xf(x)可导,于是f(x)当x≠0时可导,且
f(x)=xf’(x)+f(x)+2xcosx-x2sinx,x≠0.
由此可得f’(x)=-2cosx+xsinx,x≠0.
求积分知当x≠0时,f(x)=∫(xsinx-2cosx)dx=-xcosx-sinx+C.
利用f(x)在(-∞,+∞)上的连续性及f(0)=0,可得
[*]
于是f(x)=-xcosx-sinx不仅当x≠0时成立,而且对x=0也成立,即
f(x)=-xcosx-sinx,x∈(-∞,+∞).
故f’(x)=xsinx-2cosx,x∈(-∞,+∞).
