问题
问答题
设f(x)在[0,1]上可导,且f(x)≥0,f’(x)<0.求证:函数
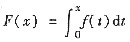 满足
满足
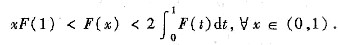
答案
参考答案:[证明] 由f’(x)<0知f(x)在[0,1]上单调减少,故[*]x∈[0,1)有f(x)>f(0)≥0,再由当x∈[0,1)时F’(x)=f(x)>0可知函数F(x)是单调增加的,又由F"(x)=f’(x)<0可知曲线y=F(x)在区间[0,1]上是凸弧,如图10-1.
[*]
由凸弧的几何特性知[*]曲线y=F(x)在线段OE的上方,即AC=F(x)>AB.在相似三角形ODE和OAb中有[*]=[*],即而[*],亦即AB=xF(1).综合得
[*]
又由定积分的几何意义知
[*]
由凸弧的几何特性及F(x)单调增加可得
[*]
最后把两个不等式连接起来即可.
