问题
单项选择题
设函数f(x)在(-∞,+∞)上可导,且y=f(x)的图形如下,
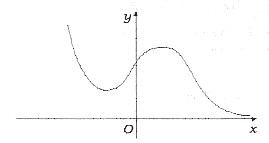
则f(x)的导函数y=f’(x)的图形为
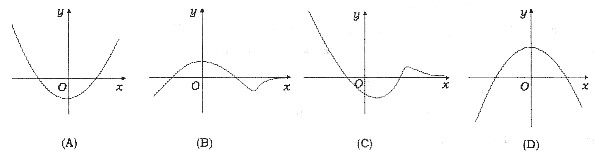
答案
参考答案:B
解析:
[分析]: 由函数y=f(x)的图形知f(x)>0,且曲线y=f*x)由单调减少变为单调增加而后再变为单调减少,从而,它的导函数的取值应由负变正,并再由正变负,这表明f(x)的导函数y=f’(x)的图形不可能是(A)与(C).
注意,若f(x)的导函数y=f’(x)的图形是(D),则由此图形可知存在常数x0>0和k>0,使得当x≥x0时成立f’(x)≤-k.设x>x0,在区间[x0,x]上对函数f(x)用拉格朗日中值定理可知,存在ξ∈(x0,x),使得
f(x)-f(x0)=f’(ξ)(x-x0)≤-k(x-x0),
于是,当x>x0时就有
f(x)≤f(x0)-k(x-x0)=f(x0)+kx0-kx,由此可见,只要[*]就有f(x)<0.所得的矛盾证实f(x)的导函数y=f’(x)的图形也不可能是(D).
综上可知f(x)的导函数y=f’(x)的图形应为(B).故应选(B).
