搜题请搜索小程序“爱下问搜题”
问题 问答题

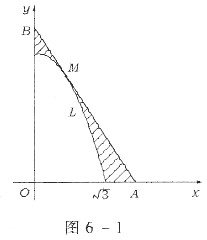
如图6-1，设曲线段L是抛物线y=6-2x2在第一象限内的部分．在L上求一点M，使过M点L的切线AB与两坐标轴和L所围图形的面积为最小．

答案

参考答案：[解] 设曲线L上点M的坐标为(x，6-2x2)，则在该点L的切线方程
Y=6-2x2-4x(X-x)．
令Y=0，可得点A的横坐标为[*]，令X=0可得点B的纵坐标为b=2(3+x2)，从而所求图形的面积为
[*]
由于[*]为一常数，可见S与ab将在同一点处取得最小值．
记[*]，不难得出
[*]
故当x=1时面积S最小，即所求点M为(1，4)．

完形填空

Bob: Good morning ! My name      Bob.

Cina:       Bob, I’m Gina.

Bob: Nice to      you, Gina. What’s your      name.

Gina:     Miller. What’s      last name?

Bob: It’s Green. My full (完全的) name is Bob Green. What’s your      number, Gina?

Gina: It’s 8876---4021.And your telephone        ,Bob?

Bob:  It’s 5793—8216. What’s that girl’s name, Gina?

Gina:      name’s Linda. What’s that boy’s name?

Bob:       name’s Tony.

小题1:A.is   B. am   C. are

小题2:A.Hi   B. Good C. OK

小题3:A. look    B. meet C. spell

小题4:A.first    B. full C. last

小题5:A. I’m    B. It’s    C. He’s

小题6:A. you B. his  C. your

小题7:A. telephone   B. class    C. room

小题8:A. name    B. card C. number

小题9:A. She B. He   C. Her

小题10:A. My B. His  C. Its
查看答案
单项选择题

缺失，余留牙正常。基牙应选（）

A.

B.

C.

D.

E.
查看答案