问题
问答题
设
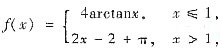 证明:f(x)在(-∞,+∞)上可导,并f’(x).
证明:f(x)在(-∞,+∞)上可导,并f’(x).
答案
参考答案:[证明] 由初等函数的连续性及f(x)的定义知,f(x)分别在(-∞,1]和(1,+∞)连续,且
[*]
于是f(x)在点x=1还是右连续的,故f(x)在(-∞,+∞)上连续.
由于g(x)=2x-2+π在x=1连续,从而f(x)也可以写成
[*]
于是f(x)在(-∞,1)内可导,在x=1左导数存在,且
[*]
同样,f(x)在(1,+∞)内可导,在x=1右导数存在,且
f’(x)=2(x>1),f’+(1)=2.
因为 f’-(1)=f’+(1)=2,故f(x)在x=1可导,且f’(1)=2.
综合得[*]
解析:
[*]
