问题
问答题
设函数f(x)在点x=0处二阶可导,且
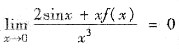 ,求f(0),f’(0)和f"(0)的值.
,求f(0),f’(0)和f"(0)的值.
答案
参考答案:[解] 设[*]
由题设知[*]
进而可得[*]
即 [*]
解析:
[分析]: 由题设函数f(x)在点x=0处二阶可导知,f(x)和f’(x)必在x=0处连续,且
[*]
再用洛必达法则,还可得到
[*]
从而,求解本题的关键是求出f(0)和f’(0).
[*]
设函数f(x)在点x=0处二阶可导,且
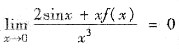 ,求f(0),f’(0)和f"(0)的值.
,求f(0),f’(0)和f"(0)的值.
参考答案:[解] 设[*]
由题设知[*]
进而可得[*]
即 [*]
解析:
[分析]: 由题设函数f(x)在点x=0处二阶可导知,f(x)和f’(x)必在x=0处连续,且
[*]
再用洛必达法则,还可得到
[*]
从而,求解本题的关键是求出f(0)和f’(0).
[*]