某IT企业计划对一批新招聘的技术人员进行岗前脱产培训,培训内容包括编程和测试两个专业,每个专业要求在基础知识、应用技术和实际训练三个方面都得到提高。根据培训大纲,每周的编程培训可同时获得基础知识3学分、应用技术7学分以及实际训练10学分;每周的测试培训可同时获得基础知识5学分、应用技术2学分以及实际训练7学分。企业要求这次岗前培训至少能完成基础知识70学分,应用技术86学分,实际训练185学分。以上说明如下表所示:

那么这样的岗前培训至少需要()周时间才能满足企业的要求。
A.15
B.18
C.20
D.23
参考答案:C
解析:
设安排编程培训x周,测试培训y周,则可以建立本题的线性规划模型如下:
目标函数:x+y,求最小值
约束条件:3x+5y≥70
7x+2y≥86
10x+7y≥185
非负条件:x,y≥0
该线性规划问题的图解法如下:
在坐标系第一象限内(因为要求x,y≥0):
画直线L1:3x+5y=7≤0 (一定通过点(0,14)与(70/3,0))
所以,3x+5y≥70表示在直线L1之上的区域。
画直线L2:7x+2y=86(一定通过点(0,43)与(86/7,0))
所以,7x+2y≥86表示在直线L2之上的区域。
画直线L3:10x+7y=185(一定通过点(0,185/7)与(20,18.5))
所以,10x+7y≥185表示在直线L3之上的区域。
上述三个约束条件以及变量非负条件组成的可行解区域见下图。
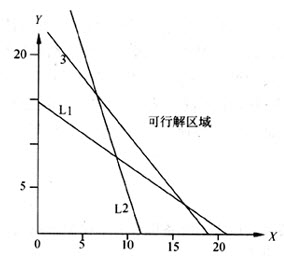
根据线性规划方法,目标函数的最小值一定会在可行解区的顶点处到达。
因此,只要考察直线L1与L3的交点以及直线L2与L3的交点处目标函数的值。
L1与L3的交点满足:
3x+5y=70
10x+7y=185
可以求出可行解区的一个顶点为(15,5),因此,x+y=20。
L2与L3的交点满足:
7x+2y=86
10x+7y=185
可以求出可行解区的另一个顶点为(8,15),因此,x+y=23。
比较这两个顶点处的x+y值,就能知道本题的最优解就是:
x=15(周),y=5(周),x+y的最小值为20(周)。

