问题
问答题
设X1,X2,X3,X4是取自正态总体N(0,4)的简单随机样本,令Y=5(X1-2X2)2+(3X3-4X4)2,求PY≤2.
答案
参考答案:[解] 因X1-2X2~N(0,20),
 ,类似地,
,类似地,
 ,又因X1-2X2与3X3-4X4相互独立,根据χ2分布的应用模式可知
,又因X1-2X2与3X3-4X4相互独立,根据χ2分布的应用模式可知
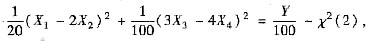

查2个自由度,上分位数为0.02的χ2分布上分位数表,可得概率
 ,即
,即
P{Y≤2}=0.01.
设X1,X2,X3,X4是取自正态总体N(0,4)的简单随机样本,令Y=5(X1-2X2)2+(3X3-4X4)2,求PY≤2.
参考答案:[解] 因X1-2X2~N(0,20),
 ,类似地,
,类似地,
 ,又因X1-2X2与3X3-4X4相互独立,根据χ2分布的应用模式可知
,又因X1-2X2与3X3-4X4相互独立,根据χ2分布的应用模式可知
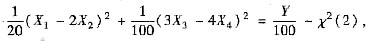

查2个自由度,上分位数为0.02的χ2分布上分位数表,可得概率
 ,即
,即
P{Y≤2}=0.01.