问题
问答题
设随机变量X的概率密度为
令Y1=X2，Y2=X3．
(Ⅰ) 分别求随机变量Y1与Y2的概率密度；
(Ⅱ) 判断Y1与Y2的相关性与独立性．
答案
参考答案：[解] (Ⅰ) 设Fi(yi)与fi(yi)分别表示Yi的分布函数与概率密度i=1，2，则当y1≤1时，F1(y1)=0；当y1≥4时，F1(y1)=1；
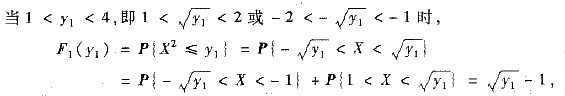
于是Y1的概率密度为
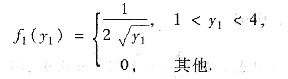
当|y2|≤1时，F2(y2)=0；当|y2|≥8时，F2(y2)=1；
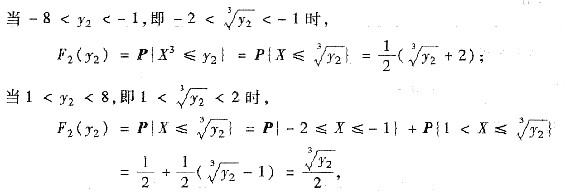
于是Y2的概率密度为
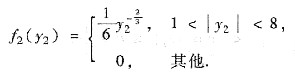
(Ⅱ) 由于X与Y2的概率密度都是偶函数，故X5与Y2的数学期望都是零，即
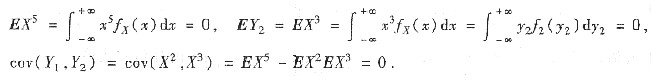
对于任意实数a，当1＜a＜2时，P{X≤a}＜1，
P{Y1≤a2，Y2≤a3}=P{X2≤a2，X3≤a3}
=P{|X|≤a，X≤a}=P{|X|≤a}，
P{Y1≤a2}P{Y2≤a3}=P{|X|≤a}P{X≤a}＜P{|X|≤a}=P{Y1≤a2}，
由于P{Y1≤a2，Y2≤a3}≠P{Y1≤a2，Y2≤a3}，且cov(Y1，Y2)=0，因此Y1与Y2不独立，但是它们不相关．