问题
解答题
（本题满分16分）已知函数f（x）对任意实数x均有f（x）="k" f（x+2），其中常数k为负数，且f（x）在区间[0，2]有表达式f（x）=x(x－2)。
⑴求f（-1）,f（2.5）的值（用k表示）；
⑵写出f（x）在[－3，2]上的表达式，并讨论f（x）在[－3，2]上的单调性（不要证明）；
⑶求出f（x）在[－3，2]上最小值与最大值，并求出相应的自变量的取值。
答案
⑴f（－1）=" k" f（1）= k（－1）=－k …………………………………………2′
f（2.5）=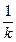
f（0.5）=×
×（－
）=－
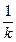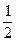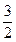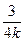…………………………4′
x∈[－2，0]时，x+2∈[0，2]
∴ f（x）=" k" f（x+2）= k（x+2）x …………………………………………6′
x∈[－3，－2）时 x+2∈[－1，0)
∴ f（x）=" k" f（x+2）= k2（x+4）（x+2）……………………………………8′
∴ f（x）=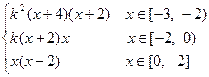
⑵f（x）在[－3，－1]上单调增，在[1， 2] 单调增
在[－1， 1]上单调减 ……………………………………………………12′
⑶x=－1，f（x）max=－k ……………………………………………………13′
k=－1，f（x）min=－1,此时x=1或x=－3 …………………………………14′
k<－1时，f（x）min=－k2，此时x=－3 …………………………………15′
－1<k<0时，f（x）min=－1，此时x="1 " …………………………………16′