设 ,若f(x)处处连续,那么a,b的值分别为()。
,若f(x)处处连续,那么a,b的值分别为()。
A.1,1
B.0,1
C.0,
D.1,
参考答案:B
解析:
先求出f(x),注意到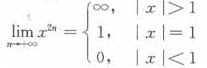
要分情形求f(x):
当|x|>1时,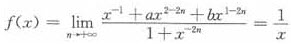 ;
;
当|x|<1时,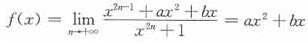 ;
;
当x=±1时,易求出f(±1),于是得
由初等函数的连续性,当|x|>1及|x|<1时,f(x)分别为初等函数,故连续,还须再看x=-1处的连续性,这是分段函数,要计算f(1±0),f(-1±0)。
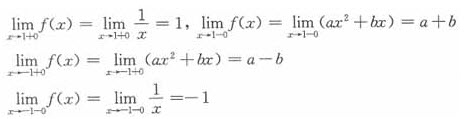
f(x)在x=1连续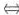 f(1+0)=f(1-0)=f(1)
f(1+0)=f(1-0)=f(1)
即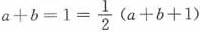 ,即a+b=1
,即a+b=1
f(x)在x=-1连续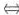 f(-1+0)=f(-1-0)=f(-1)
f(-1+0)=f(-1-0)=f(-1)
即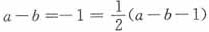 ,即a-b=-1
,即a-b=-1
故f(x)在x=±1均连续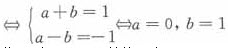
若f(x)在(-∞,+∞)连续,则a=0,b=1
故正确答案为B。
