问题
解答题
已知顶点在原点,焦点在y轴上的抛物线C截直线y=2x-1所得的弦长为210.求抛物线C的方程.
答案
x2=-y或x2=2y.
设C:x2=ay,直线与抛物线C交于点P(x1,y1),Q(x2,y2).
由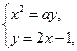
得x2=a(2x-1),即x2-2ax+a=0.
∴x1+x2=2a,x1x2=a.
而|PQ|2=(x1-x2)2+(y1-y2)2=5(x1-x2)2,
∴5［(x1+x2)2-4x1x2］=40,即4a2-4a=8.
解得a=-1或a=2.故C:x2=-y或x2=2y.
