[说明]
快速排序是一种典型的分治算法。采用快速排序对数组A[p..r]排序的3个步骤如下。
1.分解:选择一个枢轴(pivot)元素划分数组。将数组A[p..r]划分为两个子数组(可能为空)A[p..q-1]和A[q+1..r],使得A[q]大于等于A[p..q-1]中的每个元素,小于A[q+1..r]中的每个元素。q的值在划分过程中计算。
2.递归求解:通过递归的调用快速排序,对子数组A[p..q-1]和A[q+1..r]分别排序。
3.合并:快速排序在原地排序,故无需合并操作。
1. [问题1]
下面是快速排序的伪代码,请将空缺处(1)~(3)的内容填写完整。伪代码中的主要变量说明如下。
A:待排序数组
p,r:数组元素下标,从p到r
q:划分的位置
x:枢轴元素
i:整型变量,用于描述数组下标。下标小于或等于i的元素的值,小于或等于枢轴元素的值
j:循环控制变量,表示数组元素下标

参考答案:[问题1]
这是一道考查快速排序算法伪代码的分析题。快速排序是对冒泡排序的一种改进,其基本思想是:通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。快速排序最核心的处理是进行划分,即PARTITION操作:根据枢轴元素的值,把一个较大的数组分成两个较小的子数组,一个子数组的所有元素的值小于等于枢轴元素的值,一个子数组的所有元素的值大于枢轴元素的值,而子数组内的元素不排序。划分时,以最后一个元素为枢轴元素,从左到右依次访问数组的每一个元素,判断其与枢轴元素的大小关系,并进行元素的交换,如图2-30所示。
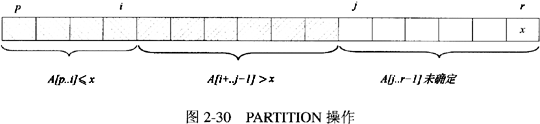
在[问题1]所给出的伪代码中,当for循环结束后,A[p..i]中的值应小于等于枢轴元素值x,而A[i+1..r-1]中的值应大于枢轴元素值x。此时A[i+1]是第一个比A[r]大的元素,因此A[r]与A[i+1]进行交换,得到划分后的两个子数组。PARTITION操作返回枢轴元素的位置,因此返回值为i+l。