问题
填空题
在抛物线y2=16x内,通过点(2,1)且在此点被平分的弦所在直线的方程是_________。
答案
8x-y-15=0
设所求直线与y2=16x相交于点A、B,且A(x1,y1),B(x2,y2),代入抛物线方程得y12=16x1,y22=16x2,两式相减得,(y1+y2)(y1-y2)=16(x1-x2).
即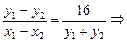 kAB=8.
kAB=8.
故所求直线方程为y=8x-15.
在抛物线y2=16x内,通过点(2,1)且在此点被平分的弦所在直线的方程是_________。
8x-y-15=0
设所求直线与y2=16x相交于点A、B,且A(x1,y1),B(x2,y2),代入抛物线方程得y12=16x1,y22=16x2,两式相减得,(y1+y2)(y1-y2)=16(x1-x2).
即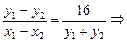 kAB=8.
kAB=8.
故所求直线方程为y=8x-15.