问题
单项选择题
考虑一元函数f(x)有下列四条性质:
①f(x)在[a,b]连续; ②f(x)在[a,b]可积;
③f(x)在[a,b]可导; ④f(x)在[a,b]存在原函数,
若用“P
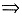 Q”表示可由性质P推出性质Q,则
Q”表示可由性质P推出性质Q,则
A.①
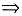 ②
②
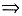 ④. B.①
④. B.①
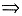 ④
④
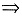 ②. C.③
②. C.③
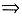 ①
①
 ②. D.③
②. D.③
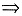 ④
④
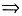 ①.
①.
答案
参考答案:C
解析:[分析一] 由基本定理,我们应知道:
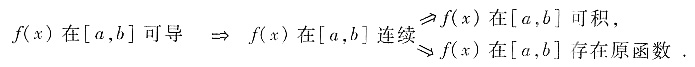
因此,应选C.
[分析二] f(x)在[a,b]可积与f(x)在[a,b]存在原函数之间无确定关系,因而
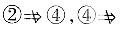 ②,即A,B不正确,
②,即A,B不正确,
可以有函数F(x),它的导函数F′(x)=f(x)在[a,b]不连续. 对此f(x),它在[a,b]存在原函数,在[a,b]不连续. 因此f(x)在[a,b]存在原函数
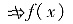 在[a,b]连续,即
在[a,b]连续,即
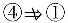 ,D不正确. 因此选C.
,D不正确. 因此选C.
令
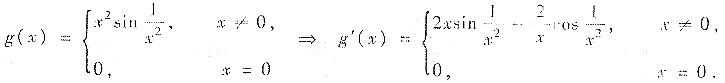
令f(x)=g′(x),则f(x)在[-1,1]存在原函数(就是g(x)),但定积分
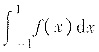 不存在,因为f(x)在[-1,1]无界. (当
不存在,因为f(x)在[-1,1]无界. (当
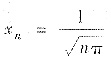 时,n=1,2,3,…;xn∈[-1,1],f(xn)=
时,n=1,2,3,…;xn∈[-1,1],f(xn)=
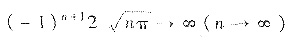 ).
).
若令
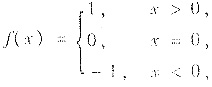 则存在定积分
则存在定积分
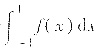 ,但f(x)在[-1,1]不存在原函数. 这表明:f(x)在[a,b]可积
,但f(x)在[-1,1]不存在原函数. 这表明:f(x)在[a,b]可积
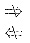 f(x)在[a,b]存在原函数,
f(x)在[a,b]存在原函数,
还是上面的f{x)=g′(x),则f(x)在[-1,1]存在原函数,但f(x)在[-1,1]不连续(x=0是它的不连续点),这表明:f(x)在[a,b]存在原函数
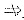 f(x)在[a,b]连续.
f(x)在[a,b]连续.
