问题
问答题
设有一容器由平面z=0，z=1及介于它们之间的曲面S所围成. 过z轴上
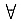点(0，0，z)(0≤z≤1)作垂直于z轴的平面与该立体相截得水平截面D(z)，它是半径
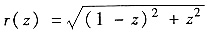的圆面，若以每秒v0体积单位的均匀速度往该容器注水，并假设开始时容器是空的.
(Ⅰ)写出注水过程中t时刻水面高度z=z(t)与相应的水体积V=V(t)之间的关系式，并求出水面高度z与时间t的函数关系；
(Ⅱ)求水表面上升速度最大时的水面高度；
(Ⅲ)求灌满容器所需时间.
答案
参考答案：(Ⅰ)由截面已知的立体体积公式可得t时刻容器中水面高度z(t)与体积V(t)之间的关系是
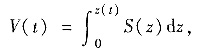
其中S(z)是水面D(z)的面积，即S(z)=π[z2+(1-z)2].
现由
及z(0)=0，求z(t).
将上式两边对t求导，由复合函数求导法得
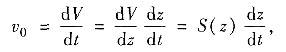
这是可分离变量的一阶微分方程，分离变量得
S(z)dz=v0dt，即
(*)
两边积分并注意z(0)=0，得
(**)
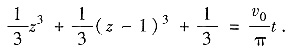(Ⅱ)求z取何值时
取最大值. 已求得(*)式即
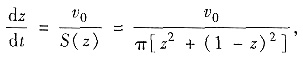
因此，求
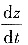取最大值时z的取值归结为求f(z)=z2+(1-z)2在[0，1]上的最小值点，由
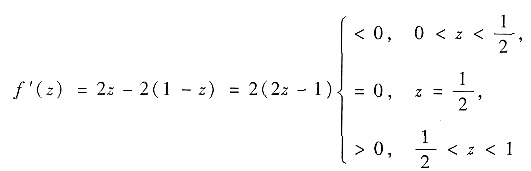
f(z)在
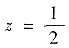在[0，1]上取最小值. 故
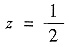时水表面上升速度最大.
(Ⅲ)归结求容器的体积，即
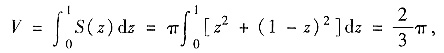
因此灌满容器所需时间为
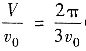(秒).
或由于灌满容器所需时间也就是z=1时所对应的时间t，于是在(**)中令z=1得
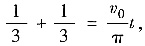即
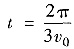(秒).