参考答案：2.

解析：[分析一] 用拉格朗日乘子法求解. 令F(x，y，z)=xyz²+λ(x²+y²+z²-4)，解方程组

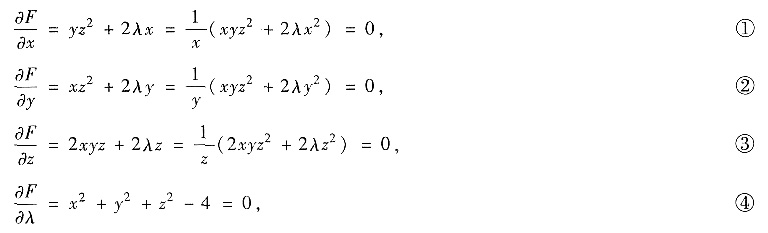
由①，②，③得y=x，

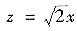，代入④得x=1，y=1，

.
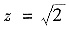因存在最大值，又驻点唯一，所以最大值为

. 填2.
[分析二] 化为简单最值问题，
由条件解出z²=4-x²-y²(0＜x²+y²＜4)，代入表达式，转化为求
u=xy(4-x²-y²)
在区域D={(x，y)|0＜x²+y²＜4}的最大值，
解

即

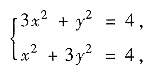
得x=1，y=1

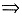u(1，1)=2.
又u在D的边界上取零值，因此

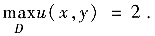填2.