问题
单项选择题
设
在点x=0处二阶导数存在，则常数a，b，c分别是
A．a=-2，b=2，c=1.
B．a=2，b=-2，c=1.
C．a=-2，b=1，c=2.
D．a=2，b=1，c=-2.
答案
参考答案：A
解析：[分析一] 本题主要考查分段函数在分界点处具有高阶导数时应满足的条件，
为了处理更一般的问题，我们考虑分段函数
其中f1(x)和f2(x)分别在较大的区间(x0-δ，+∞)和(-∞，x0+δ)(δ＞0是一个常数)中具有任意阶导数，则f(x)在分界点x=x0具有k阶导数的充分必要条件是f1(x)和f2(x)有相同的泰勒公式：
f1(x)=f2(x)=a0+a1(x-x0)+a2(x-x0)2+…+ak(x-x0)k+o((x-x0)k).
注意，在f(x)的定义中，分界点x0也可以属于f1(x)所在区间，结论是完全一样的，把上述一般结论用于本题，取
x0=0，k=2，f1(x)=ax2+bx+c，f2(x)=cos2x+2sinx,
因
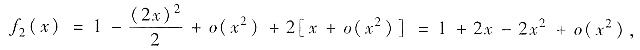
所以a，b，c应分别是a=-2，b=2，c=1，这表明结论A正确.
[分析二] 首先要求f(x)在x=0连续，即要求
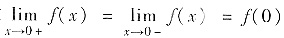，即[cos2x+
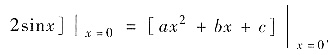得c=1. 这表明C，D不正确.
当c=1时，f(x)可写成
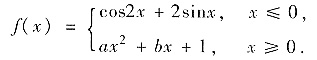
其次要求f′(0)]，即
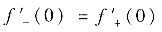，当c=1时即
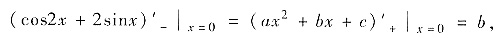
即b=2. 于是B不正确. 因此只能是A正确.
当b=2，c=1时，
