问题
单项选择题
设
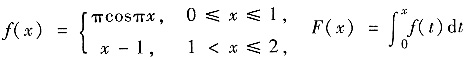，则f(x)在[0，2]上
A．有界，不可积.
B．可积，有间断点.
C．连续，有不可导点.
D．可导.
答案
参考答案：C
解析：[分析一] 先求出分段函数f(x)的变限积分，当0≤x≤l时，
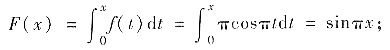
当1＜x≤2时，
即
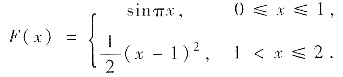
易验证F(x)在[0，2]上连续(关键是考察
).
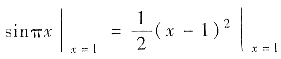当x≠1时显然F(x)可导，且
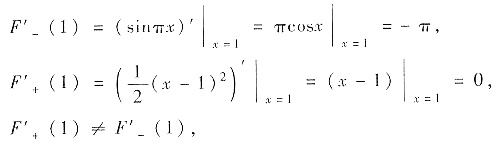
F(x)在点x=1处不可导，故应选C.
[分析二] 不必求出F(x).
这里f(x)在[0，2]上有界，除x=1外连续，x=1是f(x)的跳跃间断点. 由可积性的充分条件
f(x)在[0，2]上可积，再由基本定理
F(x)在[0，2]上连续，故A，B不对.进一步考察F(x)的可导性，当x≠1时F′(x)=f(x)，又x=1是f(x)的跳跃间断点，则F(x)在点x=1处不可导. 故应选C.
设f(x)在[a，b]上除x=x0外连续，且x=x0是f(x)的跳跃间断点，则F(x)=
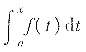在点x=x0处不可导.
[证明]此时f(x)在[a，b]上可积，当x≠x0时，
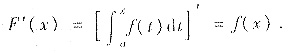
当x=x0时，考察
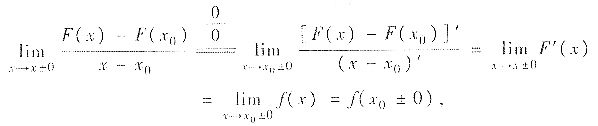
因点x=x0是f(x)的跳跃间断点，即f(x0+0)≠f(x0-0)，因此
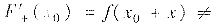
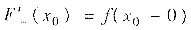，即F(x)在x=x0处不可导.