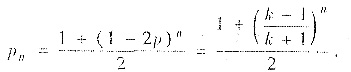参考答案：(Ⅰ)不管黑球在甲袋中还是在乙袋中，每次试验只有两种结果：取到黑球和取不到黑球，取到黑球的概率是0.1，且各次试验相互独立. 三次取球交换可以看成三次独立试验，而黑球仍在甲袋中的概率，是3次取球中黑球被取到0次或2次的概率，因此所求概率为

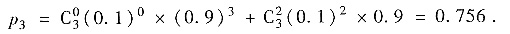
(Ⅱ)根据(Ⅰ)的分析，当交换了n次以后，黑球仍在甲袋中的事件是黑球被抓到了偶数次，也就是二项分布中所有含0.1的偶次幂项的和，故所求概率为

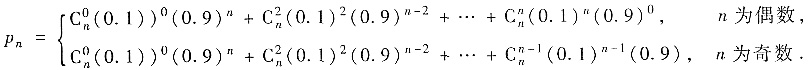
解析：本题可以用全概率公式求解，但比较麻烦，而用伯努利概型比较方便.
①(Ⅰ)是(Ⅱ)的n=3情况下的特例，我们先从n=3的简单情况入手，再推广到一般情况.
②若把乙袋中的10个白球改成9个白球，则不能用上述方法. 解题时我们的着眼点只关心与黑球运动有关的项，也就是从黑球所在的袋子中取球的情况.
设A_i：在甲袋中第i次摸到黑球(i=1，2，3)，B_j：在乙袋中第j次摸到黑球(j=2，3)，C：黑球仍在甲袋中，则

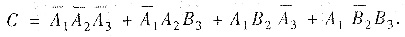
由互斥性与独立性，有

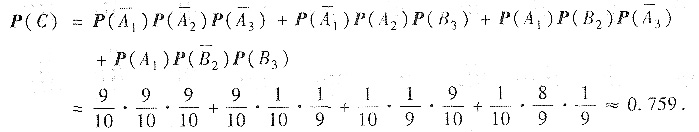
③对于(Ⅱ)，我们用全概率公式和递推法求n次试验(即取球交换)中有偶数次成功(即n次试验中黑球被抓到了偶数次)的概率p_n.
为使在n次试验中有偶数次成功，当第一次试验为成功时，则在后n-1次试验中应有奇数次失败(概率为1-p_n-1)；当第一次试验为失败时，则在后n-1次试验中应有偶数次成功(概率为P_n-1). 设每次试验成功的概率为p(失败的概率为1-p)，则由全概率公式和递推法可得

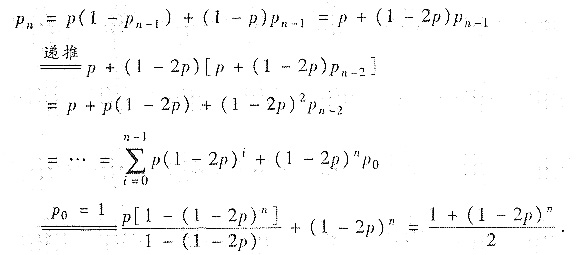
本题中

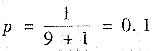，则

④将本题一般化：设甲袋中有k个白球，1个黑球；乙袋中有k+1个白球. 每次从甲、乙两袋中各随机地取一球交换放入另一袋中，求经n次交换后，黑球仍在甲袋中的概率P_n.
每一次取球交换可以看成一次独立试验，每次试验黑球被取到(交换)的概率为

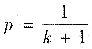没取到的概率为1-p. 如果n次试验中黑球被取到偶数次，则黑球仍在甲袋中的概率为