问题
问答题
(Ⅰ)已知由参数方程
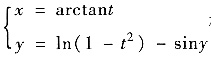确定了可导函数y =f(x)，求证：x=0是y=f(x)的极大值点.
(Ⅱ)设F(x，y)在(x0，y0)某邻域有连续的二阶偏导数，且
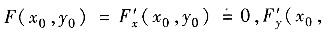
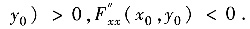由方程F(x，y)=0在x0的某邻域确定的隐函数y=y(x)，它有连续的二阶导，且y(x0)=y0，求证y(x)以x=x0为极小值点.
答案
参考答案：(Ⅰ)由x=arctant知，
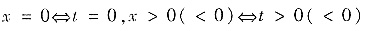. 由y=ln(1-t2)-siny知，
.
为求
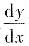，需先求
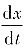与
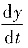，由参数方程得
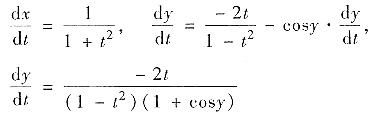
于是
其中δ＞0是充分小的数. 因此x=0是y=f(x)的极大值点.
(Ⅱ)由隐函数求导法知y′(x)满足
令x=x0，相应地y=y0得y′(x0)=0. 将上式再对x求导，并注意y=y(x)即得
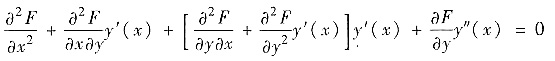
再令x=x0，相应地y=y0，y′(x0)=0，得
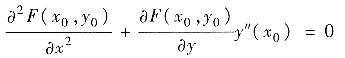
因
.
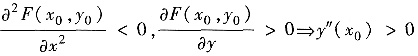因此x=x0是y=y(x)的极小值点.