问题
问答题
设f(x)连续,且满足
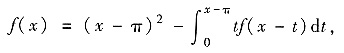
求f(x).
答案
参考答案:这是含变限积分的方程,且被积函数又含参变量,所以先作变量替换,转化为被积函数不含参变量的情形. 令s=x-t得
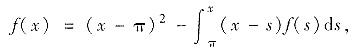
即
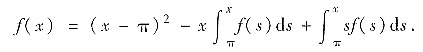 ①
①
现把它转化成微分方程问题. ①式两边求导得
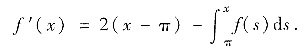 ②
②
又①式中令x=π得f(π)=0.
再对②求导得,f″(x)+f(x)=2.
在②中令x=π得f′(π)=0.
于是问题转化为求解初值问题
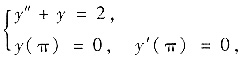 其中y=f(x).
其中y=f(x).
这是二阶线性常系数方程,显然有常数特解y*=2,于是通解为
y=C1cosx+C2sinx+2.
由
 . 解得C1=2,C2=0.
. 解得C1=2,C2=0.
因此y=f(x)=2cosx+2.
